Bubble Sort, Insertion Sort and Merge Sort in JavaScript

A computer system is a machine that connects computer hardware with computer software. In order to have a good computer with a fancy speed, it depends upon many factors, from hardware to software, single-thread computer to parallel-computer. All of those need sophisticated algorithms to run and operate. You might wonder whether algorithms are truly that important on contemporary computers in light of other advanced technologies, such as:

advanced computer architectures and fabrication technologies,
easy-to-use, intuitive, graphical user interfaces (GUIs),
object-oriented systems, integrated Web technologies,
fast networking, both wired and wireless. (WLAN, MAN, LAN, WAN, etc…)

Every time you use your computer with friendly GUIs, actually it’s really sophisticated algorithms behind the scene.

Having a solid base of algorithmic knowledge and technique is one characteristic that separates the truly skilled programmers from the novices. With modern computing technology, you can accomplish some tasks without knowing much about algorithms, but with a good background in algorithms, you can do much, much more.

Greatness starts from small steps. From the very beginning, when learning algorithms we typically begin with fundamental concepts such as sorting algorithms for sorting numbers in arrays. In this article, we will learn in detail some of the most popular sorting algorithms which are Bubble Sort, Insertion Sort and Merge Sort and identifying the time complexity each of them then finally compares those algorithms with others to help us determine what should we use in particular input size.

Bubble Sort

Bubble sort is a simple sorting algorithm. This algorithm will compare algorithms in which each pair of adjacent elements is compared and the elements are swapped if they are not in order. Due to the fact that the time complexity of this algorithm is Ο(n²) in the worst case, as we mentioned in the previous article, it’s not suitable for large data and just should be used in small input.

How does it work?

First, I’ll help you illustrate this algorithm by drawing a diagram and writing pseudocode.

Diagram:

Input: (Unsorted Array): [7,3,4,6,1,5,2]

Output: (Sorted Array): [1,2,3,4,5,6,7]

pseudocode

BubbleSort(array)
loop = array.length; // number of items
    for i = 0 to loop-1 do: // loop from index 0 to the last index array[i]

      swapped = false // lable swap = false	

      for j = 0 to loop-1 do: // a nested loop, loop from index 0 to the last index array[j]
         /* compare the adjacent elements */   
         if list[j] > list[j+1] then

            /* swap them */
            swap( list[j], list[j+1])		 
            swapped = true 
         end if    
      end for 
      if(not swapped) then
         break
      end if   
   end for
end return array

You might wonder, why we have to use a nested loop? The answer is, we observe in the algorithm that Bubble Sort compares each pair of array elements unless the whole array is completely sorted in ascending order. This may cause a few complexity issues like what if the array needs no more swapping as all the elements are already ascending.

To ease-out the issue, we use one flag variable swapped which will help us see if any swap has happened or not. If no swap has occurred, i.e. the array requires no more processing to be sorted, it will come out of the loop.

Here is how we write Bubble Sort in JavaScript language:

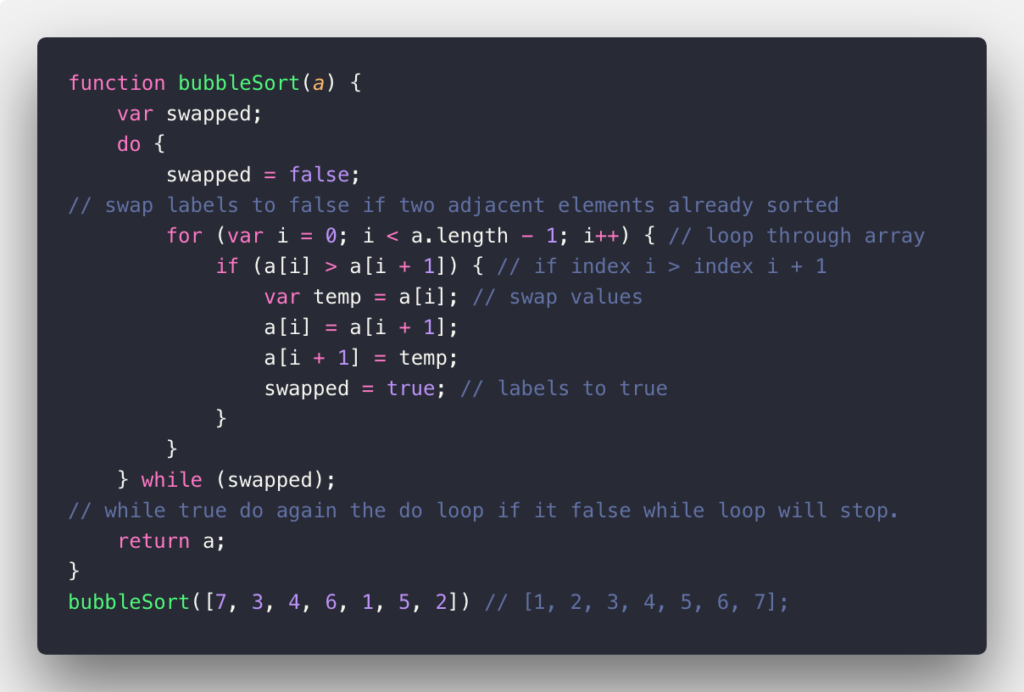
In this code, with the given array we compare two adjacent together, if the element after is less than the element before it, we swap those values and mark the swap to true. In Python and some other languages, they just have to a, b = b, a to swap two values. But here in JavaScript, we use the traditional way, which means we need an immediate variable that stores the temporary value, then we swap them. (Or another way, in case you need it: [a, b] = [b, a];, it works in JavaScript to swap two values). We do this again and again until the while loop is false when the swap value equals false. This means that every element is sorted in ascending order.

When should we use it?

As mentioned above, the time complexity of bubble sort algorithm is O(n²) The time is much longer when the input increases. So it’s just suitable for small input. If you had a large input instead, you should consider using another algorithm for sorting.

Insertion Sort

Imagining you are playing a card game you’re holding the cards in your hand, and these cards are sorted. The dealer hands you exactly one new card. You have to put it into the correct place so that the cards you’re holding are still sorted. In selection sort, each element that you add to the sorted subarray is no smaller than the elements already in the sorted subarray. But in our card example, the new card could be smaller than some of the cards you’re already holding, and so you go down the line, comparing the new card against each card in your hand until you find the place to put it. You insert the new card in the right place, and once again, your hand holds fully sorted cards. Then the dealer gives you another card, and you repeat the same procedure. Then another card, and another card, and so on, until the dealer stops giving you cards. This is the idea behind of the insertion sort.

Insertion sort is another simple algorithm for sorting. Like the Bubble Sort, it takes the array of input and compares in-place elements and swap values if it is not in ascending order, but also it creates a sub-array, which always be sorted. An element that is to be inserted in this sorted sub-list has to find its appropriate place and then it has to be inserted there. Hence the name, insertion sort. The time complexity for the worst case of this algorithm is also O(n²), thus we just should use it in the small input.

How does it work?

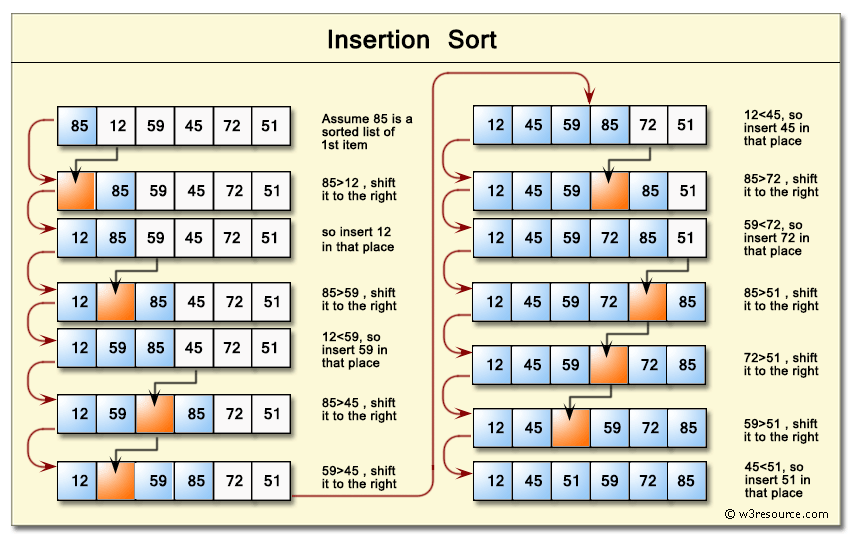
Envisioning by the insertion sort by the image and steps below:

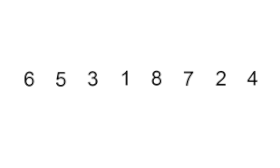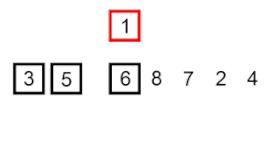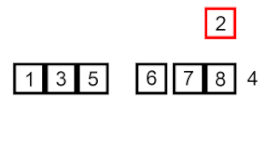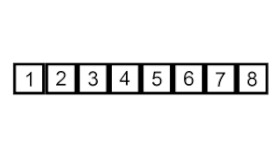
First, we have the array of [6, 5, 3, 1, 8, 7, 2, 4]
Start with the 1 index (second index) and compare it with the previous element, if it is smaller than the previous index then swap the values, and create a sub-array which is always sorted, for the next indices, continue compare its value with each element in the sub-array and insert it to the right place.
It will do it again and again until reaching the desired result.

Before	After
Step 1: [6, 5, 3, 1, 8, 7, 2, 4]	[5, 6, 3, 1, 8, 7, 2, 4] Created a sub-array with two elements [5, 6]
Step 2: [5, 6, 3, 1, 8, 7, 2, 4]	[3, 5, 6, 1, 8, 7, 2, 4] Compare 3 with each element the sub-array, put it into the beginning because it’s the smallest one. Now the new sub-array is [3, 5, 6].
Step 3: [3, 5, 6, 1, 8, 7, 2, 4]	[1, 3, 5, 6, 8, 7, 2, 4] Compare 1 with each element sub-array [3, 5, 6] then put it into the first place after comparing.
Step 4: [1, 3, 5, 6, 8, 7, 2, 4]	Now compares 8 with each element of the sub-array, because it’s the largest one so the position remains the same up to this point. [1, 3, 5, 6, 8, 7, 2, 4].
Step 5: [1, 3, 5, 6, 8, 7, 2, 4]	Now it compares 7 with each element of the sub- array [1,3 5, 6, 8]. We can see 7 is just less than 8, so we insert 7 to 8 position, also copying 8 to the next position. (swapping). Now the array is [1, 3, 5, 6, 7, 8, 2, 4]
Step 6: [1, 3, 5, 6, 7, 8, 2, 4]	Compare value 2 two the sub-array then put it between 1 and 2.
Step 7: [1, 2, 3, 5, 6, 7, 8, 4]	Finally comparing 4 with the sub-array [1, 2, 3, 5, 6, 7, 8] then put it into the right position, then we have [1, 2, 3, 4, 5, 6, 7, 8].

Look at the image below for better understanding:

pseudocode

Arr = [5, 7, 2, 1, 4, 6]
for i = 2 to Arr.length
    key = A[i]
    // A[i] is the 'key' we want to insert in the sorted sequence [1...i - 1]
    j = i - 1
    while j > 0 and Arr[j] > key
         Arr[j + 1] = Arr[j]
         j = j - 1
    Arr[j + 1] = key 
return Arr

JavaScript’s Insertion Sort Code Implementation:

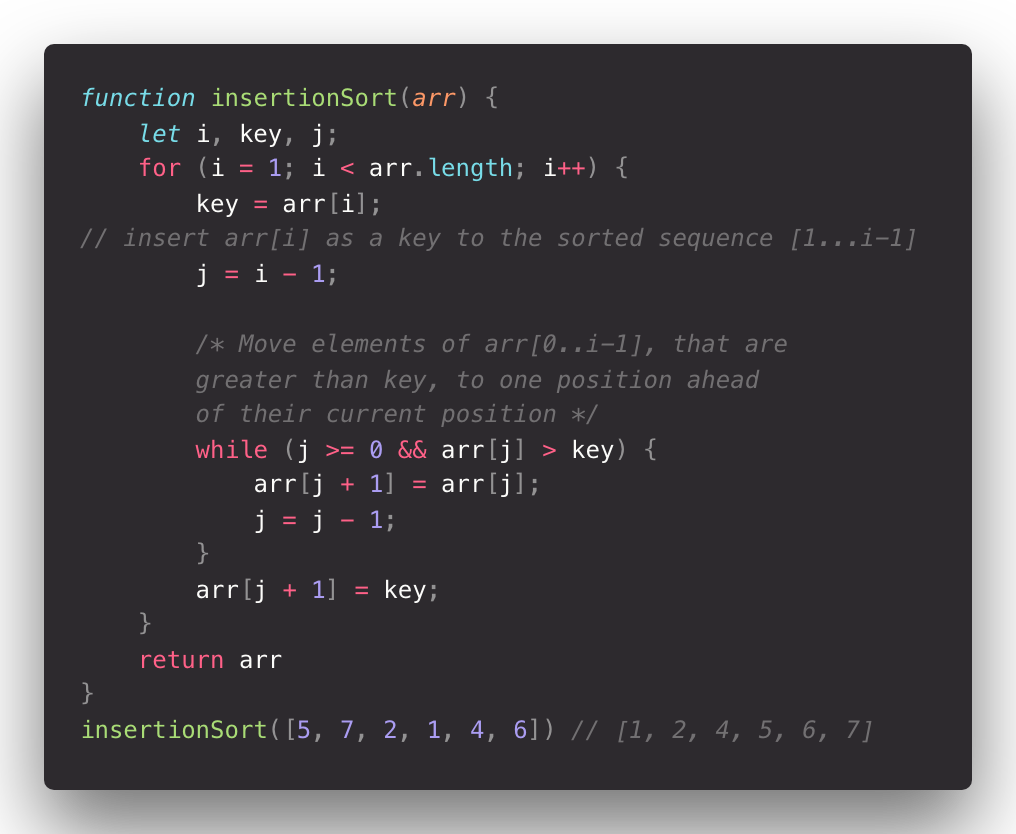
When should I use this?

It’s one of the options to substitute the Bubble Sort in case you have the small input value, it’s run faster than Bubble Sort and work well with the small number.

Merge Sort

How does it work?

With merge sort, first, we divide the list into the smallest unit (1 element), then compare each element with the adjacent list to sort and merge the two adjacent lists. Finally, all the elements are sorted and merged.

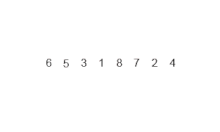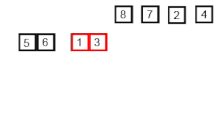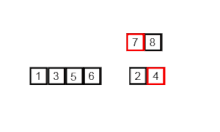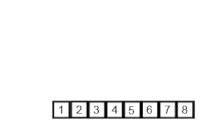
Merge sort is a divide and conquer algorithm that was invented by John von Neumann in 1945 and still used widely until today. But what is divide and conquer by the way? Divide and conquer is an algorithmic paradigm that breaks a problem into subproblems that are similar to the original problem, recursively solves the subproblems, and finally combines the solutions to the subproblems to solve the original problem. Because divide-and-conquer solves subproblems recursively, each subproblem must be smaller than the original problem, and there must be a base case for subproblems. You should think of a divide-and-conquer algorithm as having three parts:

Divide the problem into a number of subproblems that are smaller instances of the same problem.
Conquer the subproblems by solving them recursively. If they are small enough, solve the subproblems as base cases.
Combine the solutions to the subproblems into the solution for the original problem.

pseudocode in general:

func mergesort( var a as array )
     if ( n == 1 ) return a

     var l1 as array = a[0] ... a[n/2]
     var l2 as array = a[n/2+1] ... a[n]

     l1 = mergesort( l1 )
     l2 = mergesort( l2 )

     return merge( l1, l2 )
end func

func merge( var a as array, var b as array )
     var c as array

     while ( a and b have elements )
          if ( a[0] > b[0] )
               add b[0] to the end of c
               remove b[0] from b
          else
               add a[0] to the end of c
               remove a[0] from a
     while ( a has elements )
          add a[0] to the end of c
          remove a[0] from a
     while ( b has elements )
          add b[0] to the end of c
          remove b[0] from b
     return c
end func

pseudocode in JavaScript:

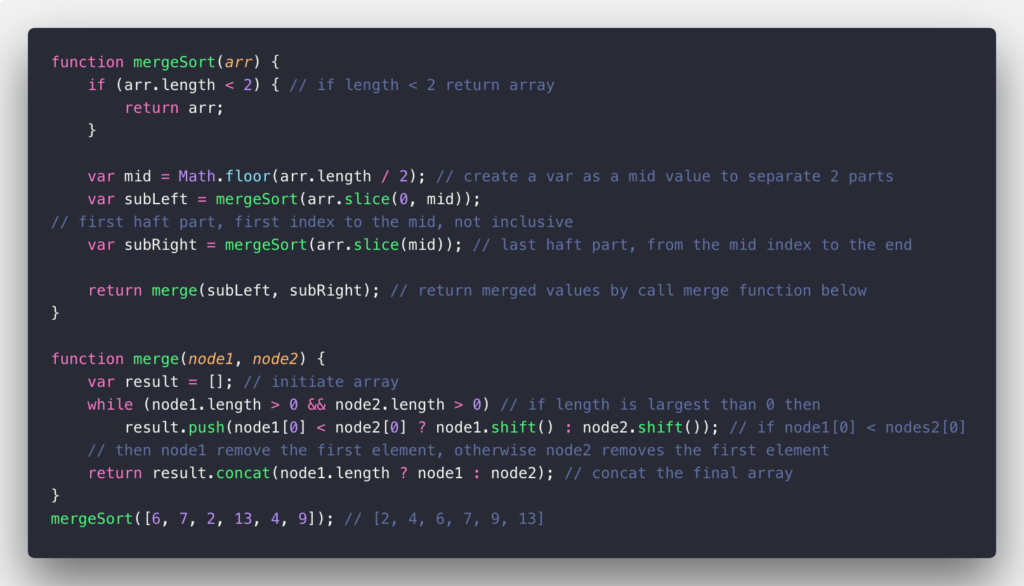
function mergeSort(array) {
  If array length < 2
    Return array
  
  Create var for middle index of array
  Create var for far left index of array
  Create var for far right index of array
  Call merge sort by using recursive function
}
Function merge (node1, node2) {
  Create var for result array

  While node1 length > 0 and node2 length > 0
    If node1[0] < node2[0]
      Shift node1 and push to result array
    else 
      Shift node2 and push to result array
  Return concat node1 or node2 (depending if node1 is empty or not)

Merge Sort algorithm in JavaScript language:

Comparison

First, we look at the running time of these 3 sorting algorithms:

Algorithm	Worst-case running time	Best-case running time	Average-case running time
Bubble Sort	$\O(n^2)$	$\O(n)$	$\O(n^2)$
Insertion sort	$\O(n^2)$	$\O(n)$	$\O(n^2)$
Merge sort	$\O(n \lg n)$	$\O(n \lg n)$	$\O(n \lg n)$

The two first algorithms above which are Bubble Sort and Insertion Sort designed to work with a small input, however, they are limited when encountering large input due to the restriction of time complexity. Merge Sort is another algorithm, which runs slower with small input but it will faster than Bubble Sort and Insertion Sort when the input becomes larger. Why? Because of the time complexity of this algorithm is different than the other two. Its worst-case scenario is $Ο(n log n)$ , which n is a constant, and hence n does not depend on the size of the input.

In order to see the difference between the efficiency of Merge Sort and Insertion Sort in the large input number. Suppose we run them on the same computer with the fast execution, 10 billion instructions per second. The time complexity of Insertion Sort is 2n², while Merge Sort is 40nlgn instructions. And they have to sort about 10 million numbers, here are the results:

Insertion Sort:

$\frac{\left(2\cdot \:\left(10^7\right)^2\right)}{10^{10}instructions\:per\:second}\: = 20000 seconds ( 20000 / 3600)$ ≈ more than 5.5 hours.

Merge Sort:

$\frac{\left(40\cdot 10^7lg10^7\right)}{10^{10}} = 0.28 second$

So, if we have 10 million number to sort, Merge Sort is faster than Insertion Sort $\frac{20000}{0.28}$ ≈ 71428 times.

Conclusion

In this article, we’ve been through learning about some popular algorithms, those time complexity and when we should use them and writing code for these using JavaScript language. Recall that Bubble Sort and Insertion Sort are used when you have the small input and Merge Sort is used for the large input. Remember to choose wisely algorithm that fit the size input to reduce the executable time and also saving the memory. The shapely developer with solid skills is outstanding from the naive ones when they can choose an effective way to solve a problem. Whenever you feel discouraged about learning algorithms or solving the new things. Overcome these obstacles is how you form your potential skills.

Facebook0 Tweet0

Bubble Sort, Insertion Sort and Merge Sort in JavaScript12 min read

Bubble Sort

How does it work?

pseudocode

When should we use it?

Insertion Sort

How does it work?

pseudocode

When should I use this?

Merge Sort

How does it work?

pseudocode in general:

pseudocode in JavaScript:

Comparison

Insertion Sort:

Merge Sort:

Conclusion