Yes, we need some math for coding21 min read
Most of us probably don’t have to write math anymore when we finish college. However, as a software developer, it’s pretty important to have some basic math skills because sometimes we do need them. After a few years of working as a software engineer for the backend role in different domains, this experience made me realize that our interaction with any website on the world’s biggest database World Wide Web (WWW) is secured and encrypted when HTTPS/SSL enabled, to make sure these protocols are secured then math is a central part of this formula, where different cryptography techniques employed such as digital signatures, one-way hashing functions, and key exchange protocols. In some domains such as Blockchain, the underlying principles of how they work technically are based on one-way hashing functions and also number theory, where informally given \(Q\) and \( P = Q * k\) then it’s computationally infeasible to find the number \(k\), in this case \(k\) could be a private key. Hashing functions could be found anywhere else as well, from designing an (immutable) caching service using different techniques such as Content-Addressable Storage (CAS) to error-detection service with check-sum to verify data integrity using MD5 or CRC (Cyclic Redundancy Check).
Discrete math is also prevalent among us, the relational database employs lots of concepts from set theory, where tables represent relation where each row is considered a tuple and all the rows inside a table are considered a set of tuples, SQL operations such as UNION, INTERSECT or EXCEPT also correspond to set-theoretic operations. Boolean algebra for control flows and decision-making when writing code and diagrams. Logic is essential to reason about the correctness of the program, for example, we can write down a first-order logical statement such as \(\forall i, j : (1 \leq i < j \leq n) \rightarrow(A[i] \leq A[j])\) meaning that for any given 2 elements inside the list, the value of element appears before must less than or equal to the value of the element after it. Graph theory applications such as finding the shortest path, a web crawler to crawl all the links to a certain webpage, or dependency resolution for database tables creation. And also finite discrete data structures that we use every day like arrays, maps, sets, or trees to manipulate data in our applications.
Probability and Statistics also play an important role in our work. For example, how we can design a hash function to minimize the chance of collision but also be space-efficient and performant at the same time? That’s when we need to use probability to calculate the chance of collision. A statistical technique such as linear regression can be used frequently as well for various kinds of tasks from user behavior prediction to response time prediction, for example, if the load is 15 concurrent requests to a web service, then what could be the expected response time for those requests?
Lately, I have had a chance to put all that I’ve learned into more serious practice and learn some new interesting subjects along the way such as data compression, Kolmogorov complexity, the concept of entropy, the new data structure named Quartet tree (an unrooted binary tree with at least 4 nodes for phylogenetic classification), designing efficient immutable hashing functions and doing linear transformation to render the 3D visualization to create a workable application. It took me quite some time to get along with them. In the end, understanding them at the conceptual level is not too distant, and writing code to test our understanding to form a coherent picture of them all probably requires some more work, but the more you get into it, the more interesting things will unfold and you will be more appreciating the fundamentals.
Boolean algebra and logic
We all know the value from the boolean type can take one exact value that’s either true or false: \(\mathbb{B} = \{ \text{True}, \text{False} \}\). Boolean algebra studies these boolean values and operations that we can do with them. We can use this in coding to make our code easier to understand by simplifying logical conditions.
The first example I want to give is that we can use De Morgan’s law to simplify our code. The rule can be expressed as follows: \(\neg (A \land B) \equiv \neg A \lor \neg B\\\neg (A \lor B) \equiv \neg A \land \neg B\)
This means the negation of A and B is the same as not A or not B. The negation of A or B is the same as not A or not B. For example, we have an if statement that looks like this:
if not (is_logged_in and has_permission):
return ACCESS_DENIEDWe can use De Morgan’s law to transform the boolean expression to something equivalent to improve the readability:
if not is_logged_in or not has_permission:
return ACCESS_DENIEDAlso, it has the extra benefit of short-circuit evaluation, meaning that if the first boolean expression is true already, then the rest of the if statement doesn’t need to be computed.
For example, we want to find out the orders in which the status is not completed and payment is not failed:
select * from orders where not (status = 'completed' and payment = 'failed')Similarly, De Morgan’s law can also be used to optimize the SQL query performance by doing the short-circuit evaluation:
select * from orders where status != 'completed' or payment != 'failed'Exclusion rules using SET operations
Let’s say we are working on an e-commerce application in which customers can order the products into the basket, and before the order is submitted, our service will check the discount exclusion rules, and remove some discounts if they’re excluded by others. In case we have 2 discounts excluding each other, then we will keep the one with higher priority. We can define what we have as follows:
- Basket \(B\): A set of discounts that are currently in the basket
- Exclusion set \(E(c)\): A set of excluded discounts when the discount \(c\) is present
- Priority function \(P(c)\): A function that returns a numerical priority value for the discount \(c\)
- Mutual exclusion: Two discounts \(c\) and \(c’\) are mutually exclusive if \(c’ \in E(c)\) and \(c \in E(c’)\)
- Unilateral exclusion: A discount \(c\) excludes the discount \(c’\) from the basket if \(c’ \in E(c)\) and \( c \notin E(c’)\)
- We also assume that there is no circular exclusion in the basket for simplicity
Let’s now write the code given the definitions and requirements in Python:
class Discount:
def __init__(self, name, priority):
self.name = name # Unique name of the discount
self.priority = priority # Priority of the discount
self.exclusions = set() # Set of discounts this discount excludes
def add_exclusion(self, discount):
self.exclusions.add(discount)
def __repr__(self):
return f"Discount(name={self.name}, priority={self.priority})"
def resolve_discounts(basket_discounts):
"""
Resolves discounts in a basket_discounts based on exclusion and priority rules.
Parameters:
basket_discounts (set): A set of Discount objects in the basket_discounts.
Returns:
set: A stable basket_discounts with all conflicts resolved.
"""
to_remove = set() # Track discounts to be removed
for discount in basket_discounts:
for excluded in discount.exclusions:
if excluded in basket_discounts: # Only handle conflicts within the basket_discounts
# Resolve based on priority
if discount.priority > excluded.priority:
to_remove.add(excluded)
else:
to_remove.add(discount)
break
basket_discounts -= to_remove
return basket_discounts
if __name__ == "__main__":
discount_a = Discount("A", 3)
discount_b = Discount("B", 2)
discount_c = Discount("C", 1)
discount_a.add_exclusion(discount_b)
discount_b.add_exclusion(discount_c)
discount_c.add_exclusion(discount_a)
basket_discounts = {discount_a, discount_b, discount_c}
stable_basket_discounts = resolve_discounts(basket_discounts)
print("Basket discounts: ", stable_basket_discounts) # Basket discounts: {Discount(name=A, priority=3)}Graph theory and dependency resolution
Graph theory concepts also can be used widely in software development, one of the very popular use cases is dependency resolution. Given a list of services that need to be deployed, here some services might depend on others, so we need to deploy services in the correct order in which the dependency of one service must be started before the service itself.
First off, we can define some graph theory definitions that we will use for this problem:
- \(G = (V, E)\)
- \(V\): Set of vertices, each representing a service
- \(E\): Set of directed edges, where \((S_i, S_j)\) means \(S_i\) depends on \(S_j\)
- Topological sorting:
- Find an order \([s_1, s_2, s_3,…,s_n]\), such that:
- \(\forall (s_i, s_j) \in E: \) service \(s_j\) is deployed before the service \(s_i\)
- If there is a cyclic dependency, then the deployment order is invalid
To find the correct order of the deployment, we’re using the directed graph to represent the services and dependencies, we will deploy the service with zero dependency first (the incoming dependency for this node is zero). We add every service to the queue, check their dependencies, and increase the incoming degree by one for each dependency of a service, once the service is deployed, it must be removed from the queue and the dependent services must update their dependency list accordingly, finally, we deploy every service in the system, otherwise,e there is some circular cycle in the graph and we cannot deploy the service. Here is the implementation in Python:
from collections import defaultdict, deque
def resolve_dependencies(services, service_dependencies):
"""
Resolve the deployment order of services based on multiple dependencies.
Parameters:
services (list): List of all services.
service_dependencies (dict): Dictionary where each service is mapped to a list of services it depends on.
Returns:
list: Deployment order of services, or raises an error if a cycle is detected.
"""
# Build graph and in-degree map
graph = defaultdict(list)
in_degree = {service: 0 for service in services}
# For each service, add its dependencies in the graph and update in-degrees
for service, dependencies in service_dependencies.items():
for dependency in dependencies:
graph[dependency].append(service)
in_degree[service] += 1
# Initialize queue with nodes having in-degree = 0
queue = deque([s for s in services if in_degree[s] == 0])
deployment_order = []
while queue:
current = queue.popleft()
deployment_order.append(current)
for neighbor in graph[current]:
in_degree[neighbor] -= 1
if in_degree[neighbor] == 0:
queue.append(neighbor)
# Check if there are nodes left with non-zero in-degree (cycle detection)
if len(deployment_order) != len(services):
raise ValueError("Circular dependency detected, deployment order is not possible.")
return deployment_order
# Example Usage
if __name__ == "__main__":
services = ["Database", "API", "Frontend", "Cache"]
service_dependencies = {
"API": ["Database"], # API depends on Database
"Frontend": ["API"], # Frontend depends on API
"Cache": ["Database"], # Cache depends on Database
"Database": [] # Database has no dependencies
}
try:
order = resolve_dependencies(services, service_dependencies)
print("Deployment Order:", order)
except ValueError as e:
print(e)
# Deployment Order: ['Database', 'API', 'Cache', 'Frontend']Modular arithmetic enables secured connections
We’re using the internet and web applications every day. The connection between our device to the web server is secured if HTTPS is enabled, so if there is a hacker tries to intercept the request and extract the payload to get our sensitive information such as the credit card numbers, this attempt will fail because the data is encrypted. To make the information secure and also both parties can verify the legitimacy of the other, math plays a central part in this process.
To make the data secure, HTTPS primarily uses symmetric key encryption for exchanging data between parties. Meaning that it uses the same key for encryption (transforming the plain data into something unreadable by humans) and decryption (transforming something unreadable to the original plain message).
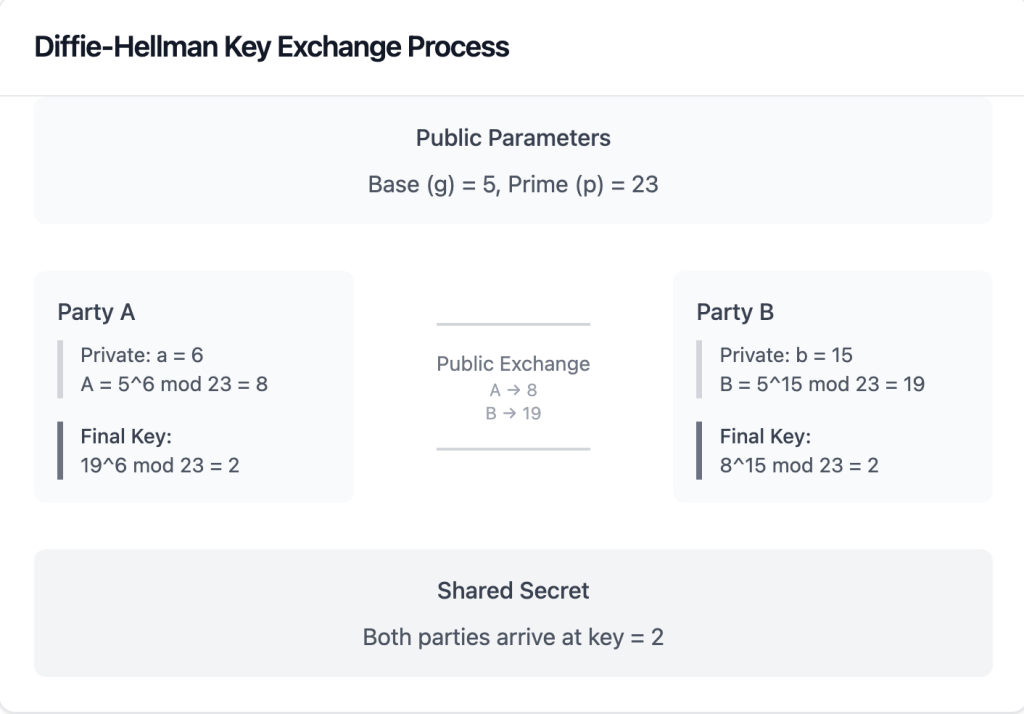
To do that, both parties must agree on the shared secret key they can use to communicate with the other before sending the actual message. But how can the shared secret key be shared through an insecure channel? That time we need to learn about the Diffie-Hellman Key Exchange (DHKE) which leverages modular arithmetic, prime numbers, and shared secret. Here are the steps on how DHKE is being used to achieve that:
- Both parties agree on public parameters that can be shared freely:
- A large prime number \(p\)
- A primitive root modulo \(p\), denoted as \(g\)
- Party \(A\) chooses a private secret \(a\) (a random number) and computes a public value and then sends it to Party \(B\):
- \(A_{public} = g^{a} mod p\)
- \(A_{public}\) is then sent to Party \(B\)
- Similarly, Party \(B\) chooses a private secret \(b\) and computes a public value from the private key and then sends it to the Party \(A\):
- \(B_{public} = g^b mod p\)
- \(B_{public}\) is then sent to the Party \(A\)
- Both parties calculate the shared secret:
- Party \(A\) computes: \(\text{Shared Secret} = (B_{public})^a mod p\)
- Party \(B\) computes: \(\text{Shared Secret} = (A_{public})^b mod p\)
- \(\text{SharedSecret}_A = (B_{public})^a mod p = (g^b mod p) ^ a = g^{ba} mod p\)
- \(\text{SharedSecret}_B = (A_{public})^b mod p = (g^a mod p) ^ b = g^{ab} mod p\)
- \(\text{SharedSecret}_A = g^{ba} mod p = g^{ab} mod p = \text{SharedSecret}_B\)
Once the shared key is obtained by both parties from the DHKE, the key then later be used in AES (Advanced Encryption Standard) to encrypt and decrypt the actual messages. Here is the Python implementation:
import random
from hashlib import sha256
from cryptography.hazmat.primitives.ciphers import Cipher, algorithms, modes
import os
# Diffie-Hellman Key Exchange
def generate_private_key():
"""Generate a private key (random number)."""
return random.randint(2, 2**16)
def compute_partial_key(private_key, g, p):
"""Compute the public partial key."""
return pow(g, private_key, p)
def compute_shared_key(partial_key, private_key, p):
"""Compute the shared key."""
return pow(partial_key, private_key, p)
# Symmetric Encryption using AES
def encrypt_message(key, plaintext):
"""Encrypt a message using AES."""
key = sha256(key.to_bytes(32, 'big')).digest() # Derive a 256-bit key
iv = os.urandom(16) # Random initialization vector
cipher = Cipher(algorithms.AES(key), modes.CFB(iv))
encryptor = cipher.encryptor()
ciphertext = encryptor.update(plaintext.encode()) + encryptor.finalize()
return iv, ciphertext
def decrypt_message(key, iv, ciphertext):
"""Decrypt a message using AES."""
key = sha256(key.to_bytes(32, 'big')).digest() # Derive a 256-bit key
cipher = Cipher(algorithms.AES(key), modes.CFB(iv))
decryptor = cipher.decryptor()
plaintext = decryptor.update(ciphertext) + decryptor.finalize()
return plaintext.decode()
# Main Demonstration
if __name__ == "__main__":
# Public parameters (agreed upon by both parties)
p = 23 # A prime number
g = 5 # A primitive root modulo p
# Party A generates private and public keys
private_key_a = generate_private_key()
partial_key_a = compute_partial_key(private_key_a, g, p)
# Party B generates private and public keys
private_key_b = generate_private_key()
partial_key_b = compute_partial_key(private_key_b, g, p)
# Both parties compute the shared key
shared_key_a = compute_shared_key(partial_key_b, private_key_a, p)
shared_key_b = compute_shared_key(partial_key_a, private_key_b, p)
# Verify the shared key is the same
assert shared_key_a == shared_key_b, "Shared keys do not match!"
# Use the shared key for encryption
message = "Hello, secure world!"
iv, ciphertext = encrypt_message(shared_key_a, message)
print("Ciphertext:", ciphertext)
# Decrypt the message
decrypted_message = decrypt_message(shared_key_b, iv, ciphertext)
print("Decrypted Message:", decrypted_message)
# Ciphertext: b'Kv\x02\xc3#o\xb2\n\x0b!%QXX\xa5\x98u\xcaj4'
# Decrypted Message: Hello, secure world!Calculate the chance of collision from a hash function
Sometimes we need to find out the total number of bits or bytes to allocate for keys in the hash table. When two different keys are mapped to the same hash value, then at this time we have a hash collision. We need to make informed decisions to minimize the chance of this event but also need to consider how much space it would take, so we can balance between the correctness and storage efficiency. Anything that happens by chance has some probability, and at that time we can apply some basic probability theory that we learned from school before implementing any hash function.
One of the real case examples is that we need to implement an efficient immutable caching strategy in which each cache entry is so small that probably we can just store them forever. When a user uploads a file to our application, we want to store some useful information from this. So later if the content of the file is not changed, then we can just use the cached value instead of doing the calculation again. We did use CRC (Cyclic Redundancy Check) to generate the cache key and cache value.
If we use the CRC-16 for our cache generation, then it would mean that we have a total \(2^{16} = 65536\) different values that the cache key could fall inside. Seems like so much space to spare, but if we already cache 999 files and there was no collision, here the chance of getting collision for the 1000th on the system can be calculated as:
\(\text{Given:} \\ n = 2^{16} \text{ (total possible hash values for CRC-16)} \\ k = 1000 \text{ (number of cache entries)} \\ \text{The probability of no collision after k entries is:} \\ P(\text{no collision}) = \prod_{i=0}^{k-1} \frac{n-i}{n} \\ P(\text{collision}) = 1 – P(\text{no collision}) \\ P(\text{collision}) = 1 – \prod_{i=0}^{999} \frac{2^{16}-i}{2^{16}} \\ P(\text{collision}) = 1 – \frac{65536 \cdot 65535 \cdot 65534 \cdot … \cdot (65536-999)}{65536^{1000}} \\ \text{Computing this exact value:} \\ P(\text{collision}) = 0.999548…\)Therefore, the probability of at least 1 collision over 1000 files if using CRC-16 is about \(99.95\%\). It’s almost certain, and we want our service can handle this number of files, that’s why we then used CRC-32 for the cache key generation purpose, with the same steps that we did above, the probability of getting at least one hash collision is just about \(0.0116\%\) for 1000 files.
Simple Linear Regression to predict the response time
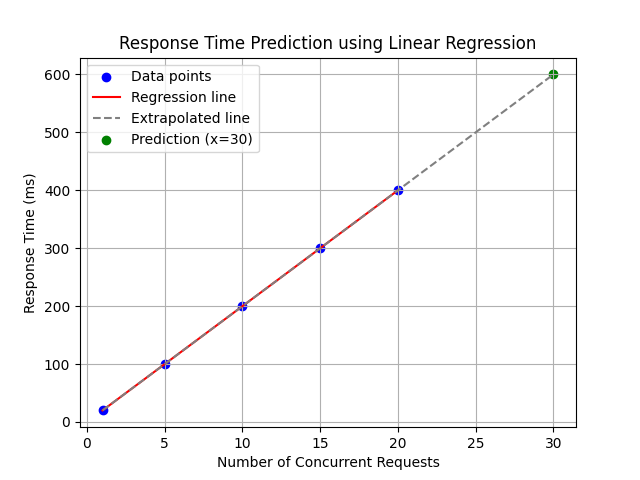
Let’s say we have a small dataset in which we track the actual response time in our system for a certain number of concurrent requests:
| Concurrent Requests ( x ) | Response Time ( y ) (ms) |
| 5 | 100 |
| 10 | 200 |
| 15 | 300 |
| 20 | 400 |
| 25 | 500 |
Now we can have a prediction on the response time in our server for 30 concurrent requests. We can model the response time and the number of concurrent requests using linear regression. Here is the formula:
\(y = \beta_0 + \beta_1 x\)We have \(y\) as the response time in our system, it’s a dependent variable and depends on the value of \(x\). The \(x\) variable that we have here is the number of concurrent requests we want in our system.
So here we know the \(x = 30\) already, we need to calculate the \(\beta_0\) and \(beta_1\) based on the formula:
\(\beta_1 = \frac{\sum_{i=1}^n (x_i – \bar{x})(y_i – \bar{y})}{\sum_{i=1}^n (x_i – \bar{x})^2}\\\beta_0 = \bar{y} – \beta_1 \bar{x}\)To find \(\bar{x}\) we just need to calculate the average of different concurrent requests we have in the left column, and similarly to calculate the \(\bar{y}\) we calculate the average response time in the right column.
Right now we have enough information to write some Python code to predict the response time for 30 concurrent requests:
import numpy as np
import matplotlib.pyplot as plt
# Dataset: Number of concurrent requests (x) and response time (y)
x = np.array([1, 5, 10, 15, 20]) # Number of concurrent requests
y = np.array([20, 100, 200, 300, 400]) # Response time in milliseconds
# Step 1: Compute the mean of x and y
x_mean = np.mean(x)
y_mean = np.mean(y)
# Step 2: Compute beta_1 (slope) and beta_0 (intercept)
beta_1 = np.sum((x - x_mean) * (y - y_mean)) / np.sum((x - x_mean)**2)
beta_0 = y_mean - beta_1 * x_mean
print(f"Linear Regression Equation: y = {beta_0:.2f} + {beta_1:.2f}x")
# Step 3: Predict response time for 30 concurrent requests
def predict_response_time(concurrent_requests):
return beta_0 + beta_1 * concurrent_requests
x_new = 30 # Number of concurrent requests
y_pred = predict_response_time(x_new)
print(f"Predicted response time for {x_new} concurrent requests: {y_pred:.2f} ms")
# Step 4: Visualization
plt.scatter(x, y, color='blue', label='Data points') # Original data points
plt.plot(x, beta_0 + beta_1 * x, color='red', label='Regression line') # Regression line
# Extrapolation
x_extrapolated = np.append(x, x_new)
y_extrapolated = beta_0 + beta_1 * x_extrapolated
plt.plot(x_extrapolated, y_extrapolated, linestyle='dashed', color='gray', label='Extrapolated line')
# Highlight prediction point
plt.scatter(x_new, y_pred, color='green', label=f'Prediction (x={x_new})')
# Plot labels and legend
plt.xlabel('Number of Concurrent Requests')
plt.ylabel('Response Time (ms)')
plt.title('Response Time Prediction using Linear Regression')
plt.legend()
plt.grid(True)
plt.show()For 30 concurrent requests we predict our system would take 600ms to respond:
Linear Transformation and 3D Quartet-tree visualization
During the time working on CompLearn 2.0, we need to create a 3D visualization of the Quartet tree to show the hierarchical cluster from the NCD matrix of different input objects. To let users zoom in and out to see the tree in different scales while maintaining the hierarchical order and relative position of each node, I need to use some linear transformation that we’ve studied in the linear algebra class to solve this problem. One particular kind of transformation that we’re using here is scaling, and it’s a linear transformation if it satisfies those 2 properties:
- Additivity: \(T(u + v) = T(u) + T(v)\) (vector addition)
- Homogeneity: \(T(cu) = cT(u)\) (scalar multiplication)
To simplify this, we can try with the 2D quartet tree when there are 2 coordinates \((x, y)\), and we use \(s\) as the scaling factor. If \(s > 1 \) then the tree expands, while if \(s < 1\) then the tree shrinks. The scaled position of \((x’, y’)\) can be computed as:
\(\begin{bmatrix}x{\prime} \\y{\prime}\end{bmatrix}\begin{bmatrix}s & 0 \\0 & s\end{bmatrix}\begin{bmatrix}x \\y\end{bmatrix}\)If we have 5 different nodes for the Quartet tree with the given positions:
\(\mathbf{P}_\text{initial} =\begin{bmatrix}0 & 0 \\1 & 1 \\-1 & 1 \\1 & -1 \\-1 & -1\end{bmatrix}\).
This means we have the first node with the value of (0, 0), the second node with the value of (1, 1), and so on. Then we try to scale the tree by a factor of 2, here is how we do it:
\(\mathbf{P}_\text{transformed} = \mathbf{P}_\text{initial} \cdot\begin{bmatrix}s & 0 \\0 & s\end{bmatrix}\)Final Positions (s = 2):
\(\mathbf{P}_\text{transformed} =\begin{bmatrix}0 & 0 \\2 & 2 \\-2 & 2 \\2 & -2 \\-2 & -2\end{bmatrix}\)The 3D Quartet tree could look something like this if we try to scale the tree by zooming in or out: