Implementing the LRU cache6 min read
A cache is a component that stores data temporarily so that further requests can be served faster. For example, the search engine might store the result from users’ queries in the cache, so later on if the same query is found, it will take the result and return it immediately to the user without doing any heavy computation or accessing the database to retrieve the data, etc…If the requested data found in the cache, we call it a cache hit, otherwise a cache miss would occur.
The cache can be implemented in different places, such as in the CPU (L1, L2, L3 cache), or it can be implemented in the main memory. However, since the cache size is limited, we cannot fit everything into the cache, also we want the cache to have some ability to add some new data and expire some data as well. That’s when the cache replacement policies come into place, when the cache is full, an algorithm must be chosen to determine which item to discard to make room for the new ones.
In this article, we want to examine one of the most popular cache replacement algorithms, which is the Least Recently Used (LRU) algorithm. Basically, this algorithm will discard the least recently used items first, this will make more sense if we look through an example:
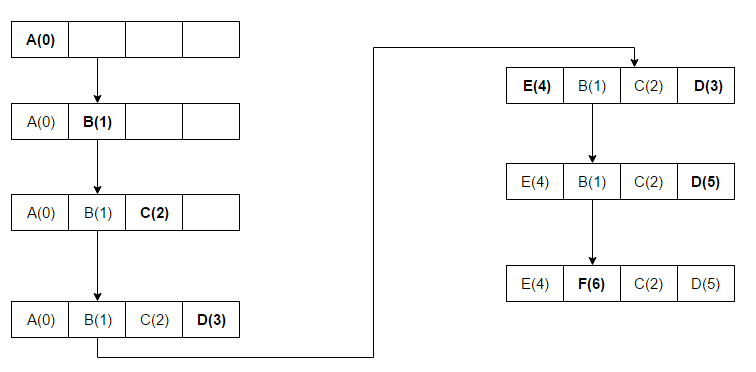
Here we have a cache size of 4, and the sequence number gets increased by one for each new access. As we can see, the first 4 items, A B C D are added to the cache without exceeding its capacity, but then we have a new element E and the cache is full, at this time, we will evict item A since it hasn’t been used for the longest time (has sequence number of 0), next item D is accessed again, here it’s already in the cache and the sequence number gets updated. Finally, item B has the lowest rank (1) get eliminated from the cache and replaced by item F. Now, if we want to add 4 new items to the cache again, we know C, E, D, F will be evicted in this order.
That’s basically the idea of the LRU cache, but how can we implement it in the application code? Let’s say we have some requirement like this:
put(k, v)should be done in O(1) timeget(k)returns the associated value with that key, otherwise return-1put(k, v)update the value for thekifkexists, otherwise add a new entry to the cache, if the cache is already full, evict the least recently used item.
We can combine 2 data structures which are a hash table and a linked list, to finish this task. The hash table can help us to look up an item cost O(1) time, while the linked list can work as a queue to manage the least recently used items and evict the LRU item in O(1) time if necessary.
Here, each time an existing item is referred to, instead of using the sequence number that we have at the beginning, the hit item will be moved to the head of the linked list. And whenever we want to discard items, we will remove them from the end of the linked list.
With that in might, we firstly create a Node class which represents a node in the linked list:
class Node {
int key;
int val;
Node next;
Node prev;
public Node(int key, int val) {
this.val = val;
this.key = key;
}
}Next we have the DoublyLinkedList class:
class DoublyLinkedList {
Node head;
Node tail;
int capacity;
int size;
public DoublyLinkedList(int capacity) {
this.capacity = capacity;
this.head = new Node(0, 0);
this.tail = new Node(0, 0);
head.next = tail;
tail.prev = head;
this.size = 0;
}
public void insertAtHead(Node node) {
Node next = head.next;
head.next = node;
node.prev = head;
next.prev = node;
node.next = next;
size++;
}
public void remove(Node node) {
Node prev = node.prev;
Node next = node.next;
prev.next = next;
next.prev = prev;
node.next = null;
node.prev = null;
size--;
}
private void moveToHead(Node node) {
if (node.prev != null && node.next != null) {
remove(node);
}
insertAtHead(node);
}
private Node removeTail() {
Node node = tail.prev;
remove(node);
return node;
}
}
Here in our DoublyLinkedList class, the head will be the most recently used item, while the tail will be the least recently used item. Our linked list has references to the head and tail elements, note that here the head and tail are just dummy nodes. Elements added to the beginning will be placed after the dummy node, the same rule applied when removing elements from the end, here our removal candidate will be the node placed before the tail. Once an existing element gets referenced, it will then be moved at the beginning, when the cache is full, we simply call the removeTail method which will remove an actual node at the end.
Next, we use the existing hash table implementation in Java to hold key-value pairs of our cache:
private Map<Integer, Node> map;Finally, we create the LRUCache class, which contains 2 methods, get and put and underlying it uses 2 data structures that we’ve just had in the previous steps.
public class LRUCache {
...
private DoublyLinkedList linkedlist;
private Map<Integer, Node> map;
public LRUCache(int capacity) {
this.linkedlist = new DoublyLinkedList(capacity);
this.map = new HashMap<>();
}
public int get(int key) {
if (!map.containsKey(key)) {
return -1;
}
Node node = map.get(key);
linkedlist.moveToHead(node);
return node.val;
}
public void put(int key, int value) {
Node node = map.containsKey(key) ? map.get(key) : new Node(key, value);
node.val = value;
linkedlist.moveToHead(node);
map.put(key, node);
if (linkedlist.size > linkedlist.capacity) {
Node tail = linkedlist.removeTail();
map.remove(tail.key);
}
}
}In the get method, we simply check whether the cache contains a key or not, if there is a cache miss, we return -1, otherwise, we return the value associated with that key, and move the matching node to the beginning of the linked list.
For the put method, we create a new node if it doesn’t exist yet, and then make it the most recently used element by moving it to the beginning of the linked list. If adding a new node to the linked list exceeds its capacity, we evict the least recently used element in both our map and list.