Optimizing NCD computation with caching using Cyclic Redundancy Check (CRC-32)13 min read

Introduction

Recently, we’ve been working on building the next version of CompLearn – a scientific toolkit using Normalized Compression Distance (NCD) to find similarity patterns in any kind of data. Simply put, it’s a pair-wise similarity metric (when using a normal compressor) in which it compares the similarity between 2 objects based on their compressed size and has the following properties:

1. It’s symmetric: \( NCD(x, y) = NCD(y, x) \) NCD is unchanged by changing the order of x and y
2. It satisfies the triangular inequalities: \( NCD(x, y) + NCD(y, z) >= NCD(x, z) \)
3. \(NCD(x, y)\) will be between \([0, 1]\), where 0 indicates two objects are identical while 1 means two objects are completely different.

Here is the NCD formula:

Where:

1. \(C\): is a normal data compressor.
2. Since x and y are files or strings
3. We write the concatenation of x and y as xy
4. The C function returns the compressed size in bytes of the input.
5. \(C(xy)\): is the compressed size of x and y when concatenated together
6. \(C(x)\) is the compressed size of x, while \(C(y)\) is the compressed size of y
7. \(max(C(x), C(y))\) in the denominator gives us the maximum compressed size between x, and y. By dividing this value, we can have our \(NCD\) score fall between 0, and 1 (hence the term “normalized”)

Why move beyond GZIP?

The first compression algorithm we adopt to calculate the NCD score is GZIP, but the problem with GZIP is that it only works well with small files, i.e. \(size(x) + size(y) <= 32 KB \), if two files concatenated together are larger than 32KB then the NCD score might not be accurate. This is because NCD calculates the similarity score by relying on the underlying compression algorithm to detect the redundancy in the data, and here if we use GZIP and the pair file size is larger than the window that it can accept, then some part of the input might be ignored. If we have two files both 100KB in size, but the window is only 32KB, then we can’t see if the two files are identical because the window is too small.

We started with gzip because it’s the simplest compressor. User feedback let us know there was interest in analyzing larger files so we have started to add more advanced and modern data compressors with larger or unlimited window sizes. The next option we added was to use LZMA, which is also a dictionary-based compression algorithm like GZIP but offers a much wider window size of up to 4GB, so the NCD score could correctly reflect a much larger file size. However, LZMA could be 10 times slower than the GZIP counterpart, and our CompLearn toolkit lets users input multiple files at once and file sizes could be large. So there are some valid motivations to add some small optimizations to make the LZMA version work faster even with a more demanding workload.

Some small optimization

The first thing I want to point out is that there is a property \(NCD(x, x) = 0 \) because identical content should always have an NCD score near 0. If there are 5 different files, then the NCD matrix would have \(n * n = 25\) entries with \(n\) as the number of input files. As mentioned before, \(NCD(x, y) = NCD(y, x)\) since they are symmetric, so we can just calculate the \(NCD(x,y)\) and use this value to \(NCD(y, x)\). These small optimizations can help quite a bit when the input size becomes large.

Now we want to try out NCD with the LZMA compression option, our input files now are some translation versions of the Universal Declaration of Human Rights (UDoHR) in 4 different languages, and each file is about 200KB. However, it took me around 22 seconds to get the NCD scores showing from the moment it started calculating, it’s really bad in terms of user experience. We’re planning to add some faster compression algorithms really soon, but another optimization we can do before that can bring the mutual benefit to all the compression algorithms we will be adding, later on, is to add some caching to the NCD calculator. Here, when the user uploads the files into our system, the first time there is no cache then some real computation needs to be performed. However, if later some of the same file content is used again, we need to create a mechanism to skip these file calculations to render a better performance. So here when considering 2 files \(x, y\), we can cache the compressed size of \(x\), \(y\), and \((xy)\) so there is no need for redundant calculation. But there is one problem, what if any content of these files gets changed and our cache is not smart enough to figure out that this same file name has different content?

Cyclic Redundancy Check

That’s where the Cyclic Redundancy Check (CRC) comes into play. This is a lightweight error-detection algorithm that computes a fixed-size checksum of a given input. This is primarily used for error detection but we can also use this in our NCD calculator as well to check whether our input file content has been changed or not. So there are 2 properties of the CRC that we should keep in mind:

1. If the content of 2 files is different, then it indeed will generate 2 different hashes.
2. If the hashes between 2 files are the same, the content might be identical (but not definitely due to hash collision)

Here we loop through all pieces inside the content of each file and compute the CRC hash value. Even though it’s \(O(n)\) time complexity for calculating the CRC, it’s extremely fast since it uses the \(XOR\) operation on each computation. Besides the performance consideration, we also want to make sure it functions correctly when used as a caching mechanism in our CompLearn toolkit because the number of bits we use for CRC will determine how many different values our CRC algorithm could hold since we are using it in the bit level.

First, if we choose 8 bits, e.g. CRC-8, then we have a total of \(2^8 = 256 \) different values our cache can hold, then what is the probability of inputting 5 different files to our CRC-8 and there is no collision?

Let’s say we have \(x_1, x_2, x_3, x_4, x_5\) to represent the file content that we have. And \(CRC(x_i)\) will give us the hash value of the file with the content \(x_i\). From the birthday problem, we can find out the probability of no collision as:

The first file content will have 100% no collision since there is no hash preceding it, so it’s \(\frac{256}{256} = 1\). The second one needs to avoid the first hash, and then the probability of no collision in the second would be \(\frac{256 – 1}{256}\). With the same pattern, the last one would be \(\frac{256-4}{256}\). Because the hashes of each file are dependent, so we need to use the product rule of probability in this case, rendering this final result:

So it’s pretty safe to say that if there are 5 files there are about \(96\%\) of probability that there is no collision. However, what if we try out with 20 files instead? So our calculation would look like this:

\(P = \frac{256 \times 255 \times 254 \times \dots \times (256 – 19)}{256^{20}} = \prod_{i=0}^{19} \left( 1 – \frac{i}{256} \right) = 0.47\). So there is just about \(47\%\) chance that there is no collision if we have 20 files.

Even with just 20 files, it has shown us the probability of high collision, and the problem could get worse since we want our cache to be there mostly forever, since simply just a very small mapping between the hash value to the content size (e.g. hashVal -> fileContentSize), so if users keep using our system, the number of cached files would become huge, potentially up to thousands of files (here we don’t store the file content, just the file size of it). So let’s try with CRC-16 and see what the chance of no collision is if there are 1000 files:

So if we have 995 cached files already and then we have 5 new files that we want to find the similarity score of, then almost with certainty that there is a collision since the probability of no collision is even less than \(1\%\), which then corrupts the NCD metric.

That’s why we need a bigger power of 2 value, in this case, we would pick 32 bits (i.e. CRC-32), which means we have a total of \(2^{32}\) values to be used. With the same formula to be used, we then obtain the value of around \(99.9\%\) probability of no collisions for 1000 files and over \(90\%\) probability of no collision for 30000 files. So that’s pretty practical to use this bit value for CRC as our next version is still in its inception and there is much more to come.

CRC-32

We have finalized the use of 32 bits for CRC, now let’s dive into the technical details of how it works under the surface level. But first, let’s revise some concepts in binary arithmetic, there are 3 fundamental operations we’re probably familiar with when dealing with bit manipulation, let’s have 2 decimal values \(x\:and\:y\) and the \(b_x\) is the binary representation of \(x\) and \(b_y\) is the binary representation of \(y\), then these properties will always hold:

\(b_x\:AND\:b_y = b_z\) where \(b_z\) always \(<= min(b_x, b_y)\)

\(b_x\:OR\:b_y = b_z\) where \(b_z\) always \(>= max(b_x, b_y)\)

However, with the \(XOR\) operation, the result of 2 binary numbers will not always follow the larger or smaller pattern, instead, it’s seemingly random in nature, which is perfectly fit for error detection and capture changes in the data.

Conceptually, the CRC-32 algorithm performs polynomial division in the Galois Field GF(2): it’s a mathematical system consisting of just 2 elements 0 and 1 (i.g. \(GF(2) = \{0, 1\}\)), where the input message (augmented with zeros) serves as the dividend and a standardized generator polynomial serves as the divisor. In this field, addition and subtraction are equivalent and implemented using the XOR operation.

The algorithm processes the input message bit by bit, maintaining a running calculation. When the most significant bit (MSB) of the current value is 1, it indicates that the current polynomial degree equals or exceeds the generator polynomial’s degree. At this point, the algorithm performs polynomial arithmetic by left-shifting the current value (multiplication by x) and then applying an XOR operation with the generator polynomial. This process continues iteratively until all bits of the augmented message have been processed.

The final result is the remainder of this polynomial division (this is done through addition and subtraction using the \(XOR (\oplus)\) operation). The standard generator polynomial of CRC-32 has the following form:

\(G(x) = x^{32} + x^{26} + x^{23} + x^{22} + x^{16} + x^{12} + x^{11} + x^{10} + x^8 + x^7 + x^5 + x^4 + x^2 + x + 1 \).

At any position \(x_i\) the value must either be 1 or 0. The value of \(x_i\) will be 1 if the position \(i\) presents in the RHS of the above expression. In this case, \(x_{32} = 1\), \(x_{26} = 1\), \(x_{23} = 1\) and so on. If the position \(i\) is absent from the expression, then the according binary representation on this position will be 0. From this rule, we can now obtain the full 32 bits of the generator polynomial as \(100000100110000010001110110110111\) which will equal to \(0x04C11DB7\) in the hexadecimal format.

CRC-32 Implementation

Let’s implement the basic version of CRC-32 in Typescript:

class BasicCRC32 {
    private static readonly POLYNOMIAL = 0x04C11DB7;
    private static readonly INITIAL_VALUE = 0xFFFFFFFF;

    public static calculate(data: Uint8Array): number {
        let crc = BasicCRC32.INITIAL_VALUE;
        for (const byte of data) {
            // Process each byte
            crc ^= (byte << 24);
            // Process each bit of the byte
            for (let bit = 0; bit < 8; bit++) {
                if (crc & 0x80000000) {
                    crc = ((crc << 1) ^ BasicCRC32.POLYNOMIAL) >>> 0;
                } else {
                    crc = (crc << 1) >>> 0;
                }
            }
        }
        return (crc ^ BasicCRC32.INITIAL_VALUE) >>> 0;
    }
}

Inside the calculate function, we first assign the CRC to the initial value with 32 bits set to 1. Inside the loop, we go through each byte in order. The (byte << 24) will shift the current byte 24 positions to the left, leaving the MSB with the byte value, and the rest 24 bits will be filled with 0. Then we \(XOR\) with the current CRC value, without this the information of the previous calculation will be lost.

We can perform the polynomial division when the divisor polynomial has a degree less than or equal to the dividend polynomial. In the inner loop, we check whether the MSB of the current \(CRC\) has the same degree as the generator polynomial by \(ANDed\) with the \(0x80000000\). If that’s the case, we shift left one bit each and do the \(\oplus\) operation with the polynomial constant. Otherwise, we just shift one bit left to process the next bit without \(XORing\). In the end, we flipped the CRC value one more time to obtain the final result since it’s part of CRC-32 specification, the \(>>>\) operation will make the CRC value always non-negative.

CompLearn 2.0 with the CRC-32

In the custom file upload tab, I uploaded 4 different language files, i.e. English, French, Russian, and Spanish to measure their similarity by the translations of UDoHR in those languages, the first NCD calculation with LZMA output this matrix and quartet tree after 22 seconds:

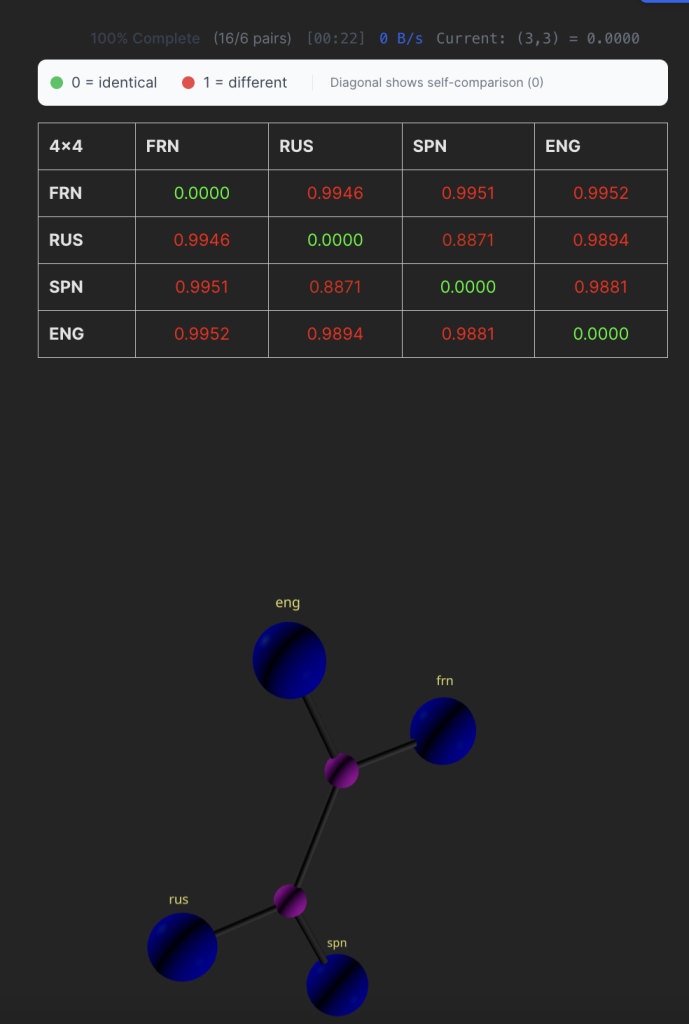
Next, we want to add Vietnamese to the tree and still keep the existing ones, here in this case, we already have the NCD values of the computed languages cached using CRC-32, so 16 entries in the matrix stay intact and now we only need to compute 9 more entries since we have total of 5 * 5 NCD entries when the fifth language is added:

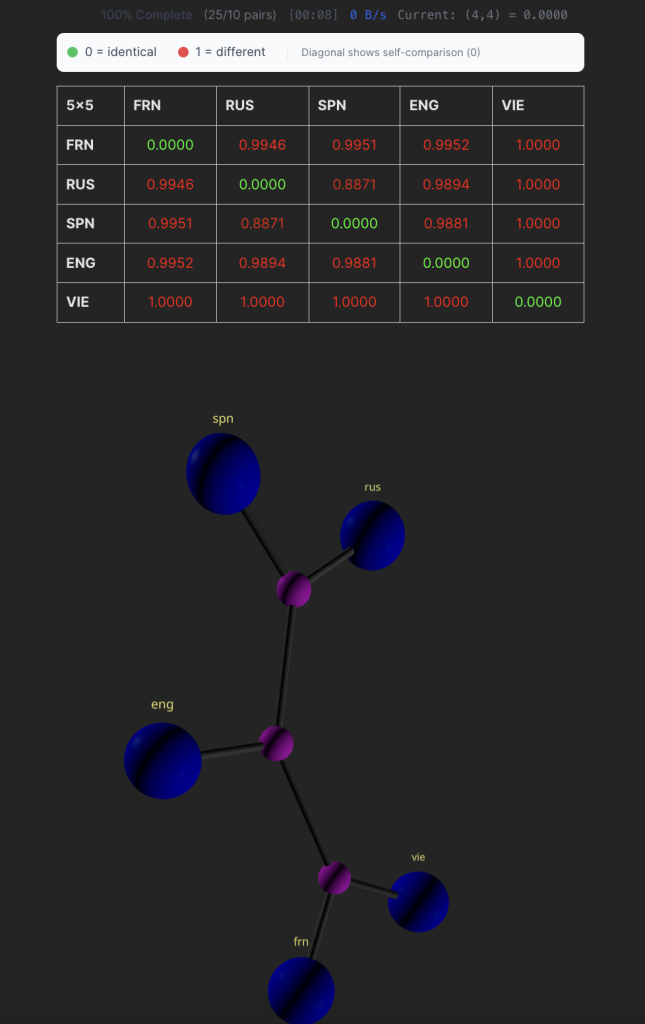
Only 8 more seconds to compute the 9 new entries without caching it would take us 30 seconds more for these translations.

Even 8 seconds is not a good user experience, but we’re more inclined to demonstrate the applicability of the CRC-32 for caching in our NCD calculator when we can apply some bit of engineering and computer science to our real work. We’re aware of loading time issues for some of the compression algorithms such as LZMA showing here, we will address this problem really soon and there will be more interesting blog posts about our science craft in the future! Thanks for reading!