Quicksort algorithm – Lomuto partition scheme

There are a multifarious number of sorting algorithms have been proposed and being used nowadays. Perhaps you’re already familiar with some sorting algorithms such as Bubble Sort, Selection Sort, or Insertion Sort. These sorting algorithms have some similarities, the first thing is they’re being taught in the college all the time in some introductory courses, the second thing is they are quite easy to implement, however, the most prominent correlation between them is they all labeled as not-so-efficient sorting algorithms with the average and worse case of $O(n^2)$ .

In this article, I want to introduce to you one of the most efficient sorting algorithms of all time, far better compared with these algorithms above, named Quicksort. This sorting algorithm was invented by Tony Hoare in 1959 (which was a really long time ago but still widely used today!). At the end of this article, I hope you can understand what is the quicksort algorithm, how it could be implemented, its time and space complexity.

Table of Contents

“Divide-and-conquer” technique

Quicksort works based on the “divide and conquer” paradigm which means quicksort is a recursive algorithm. A divide and conquer is a paradigm in which the problem is divided into multiple subproblems with the same type, each subproblem is then solved independently, and finally, we combine the sub solutions of all subproblems together to solve the original big problem.

Quicksort applies the divide and conquer paradigm as follow:

First, pick an element, called pivot from the array.
Partitioning by dividing the array into two smaller arrays. Rearrange elements so which all elements which are less than the pivot will be moved to the left array, all elements greater than the pivot will be moved to the right array.
Then recursively apply these 2 steps in smaller sub-arrays until all of them are sorted.

Understand Quicksort

There are various different implementations for the Quicksort algorithm, here we examine the pseudocode from one of them, which is used to sort elements from low to high of an array A:

/* Lomuto partition scheme for quicksort algorithm */

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p := partition(A, lo, hi)
        quicksort(A, lo, p - 1)
        quicksort(A, p + 1, hi)

algorithm partition(A, lo, hi) is
    pivot := A[hi]
    i := lo
    for j := lo to hi do
        if A[j] < pivot then
            swap A[i] with A[j]
            i := i + 1
    swap A[i] with A[hi]
    return i

Let’s make things more clear, for example, we have the array [2, 9, 7, 6, 4, 3, 8, 5]. The first step is we need to pick a pivot element, for the sake of simplicity, we pick the last element as the pivot, so our pivot here is 5. Then the second step is we move all elements that are less than 5 to the left and all the greater to the right, after partitioning, our array might look like: [2, 4, 3, 5, 9, 7, 8, 6], elements are placed in the correct positions with respect to the pivot, however, as we can easily notice, the order of elements on the left and right intervals are not correct. In the third step we recursively apply these two steps to these sub-arrays, now we have the left sub-array[2, 4, 3], then we pick 3 as the pivot, then reorder the subarray, now it will become [2, 3, 4], then on the right subarray [9, 7, 8, 6] 6 is picked the pivot, the right subarray then become [6, 7, 8, 9].

Here is how our array being changed after the first call to the partition function:

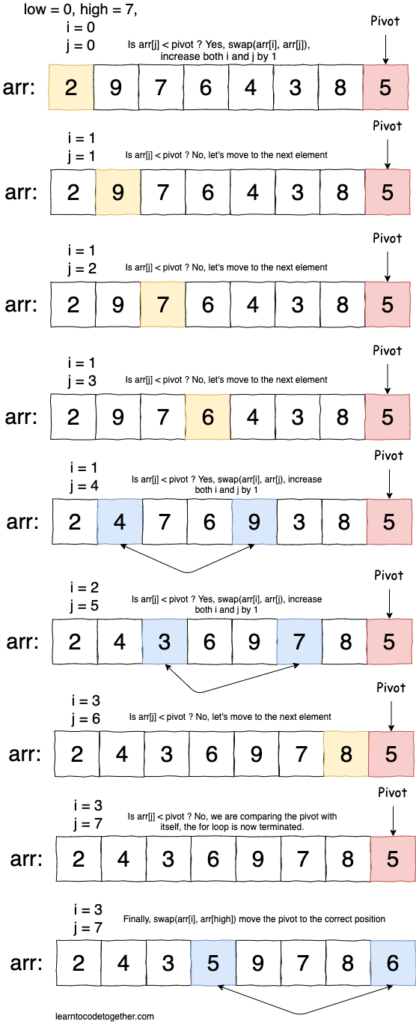
After the first call to the partition function is settled, the pivot is now placed correctly and the position of the pivot is obtained. Then, we can further call the quicksort function on the left and right of the pivot.

Now the left subarray has 3 elements [2, 4, 3] and 3 is picked as a pivot, after partitioning, this subarray will then become [2, 3, 4] and considered sorted. The index for the pivot now is 1, by this time, no more recursive calls on the smaller arrays of this subarray will be made because we have reached the base case, the condition (lo < hi) in the pseudocode is no longer true (quicksort(arr, 0, 0), and quicksort(arr, 2, 2)).

The right subarray is totally sorted [6, 7, 8, 9], after moving the pivot to the precise position, we get 4 as the index to further divide this array to more sub-arrays (notice that the index here is the index of this element on the original array). Now we then call quicksort on its left, quicksort(A, 4, 3), no more recursive call is made on the sub-left, on the right, we again apply quicksort(arr, 5, 7), the recursive process is then continued again until the base condition lo >= hi is met.

Quicksort simple implementation in Java

Let’s implement the Quicksort algorithm in Java using Lomuto partition scheme:

public class QuickSort {
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int partition = partition(arr, low, high); // get the correct position of the pivot
            quickSort(arr, low, partition - 1); // call quickSort on the sub-left array
            quickSort(arr, partition + 1, high); // call quickSort on the sub-right array
        }
    }

    public static int partition(int[] arr, int low, int high) {
        int pivot = arr[high]; // pick the last element as the pivot
        int i = low; // initially set i to low
        for(int j = low; j < high; j++) { // loop through all array elements
            if (arr[j] < pivot) {
                swap(arr, i, j); // move elements less than pivot to the correct order by swapping arr[i] with arr[j]
                i++; // increase i to the next array position
            }
        }
        swap(arr, i, high); // swap the pivot to the correct position
        return i; // return the index of the pivot
    }

    public static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

Let’s create some tests:

public static void main(String[] args) {
        int []arr = new int[10];
        for(int i = 0; i < 10; i++) {
            arr[i] = new Random().nextInt(100);
        }
        System.out.println("Before sorting: ");
        System.out.println(Arrays.toString(arr));
        quickSort(arr, 0, arr.length - 1);
        System.out.println("After sorting: ");
        System.out.println(Arrays.toString(arr));
}

Output:

Before sorting: 
[73, 49, 87, 74, 51, 40, 11, 42, 85, 98]
After sorting: 
[11, 40, 42, 49, 51, 73, 74, 85, 87, 98]

Some notes about Quicksort

Quicksort is an unstable sorting algorithm, meaning the order of the same elements is not preserved before and after performing sorting. There are a number of different implementations for Quicksort, what we’ve learned is one of them. One of the popular implementations for Quicksort is Hoare partition scheme, in which it uses two indices that start at the ends of the array being partitioned, each index moving forward each other, elements with wrong orders will be swapped until they detect an inversion.

Quicksort time and space complexity

Time complexity

In the ideal case, each time we perform partition by divide the array into 2 nearly equal sub pieces, this means each recursive call processes a list of half the size, hence, we only need $O(logn)$ calls before we reach the list of size 1, meaning the depth of the recursive tree is $O(logn)$ , each level of call only needs $O(n)$ time altogether. Thus, the best case complexity of this algorithm is $O(nlogn)$ . The time complexity for the average case is also $O(nlogn)$ .

However, if the quicksort is implemented using the Lomuto partition scheme, the worst case of this algorithm is degraded to $O(n^2)$ time. The most unbalanced partition occurs when one of the sublists returned by the partitioning routine is of size $n-1$ , this might happen when the pivot is the smallest or the largest element on the array. When this happens on every partition, each recursive call will call on the list with the size less than one of the previous list, then the recursive tree will have a linear chain of $n-1$ nested calls. For the first call, there will be $O(n)$ time on this call, the next will have the time complexity of $O(n-1)$ , etc…For the $i-th$ recursive call, the time required for this call is $O(n-i)$ , and $\sum _{i=0}^n\:\left(n\:-i\right) \in O(n^2)$ . Thus, Quicksort takes $O(n^2)$ in the worst case.

Space complexity

Quicksort is an in-place sorting algorithm, meaning no auxiliary data structure is needed to complete its function, when carefully implemented, the space complexity of Quicksort is $O(logn)$ even in the worst case, each partition only takes a constant space of $O(1)$ and there will be $O(logn)$ for all recursive calls.

However, in the naive approach, the space required for this algorithm is $O(n)$ .

To learn more about Quicksort and more precise and rigorous mathematical proofs, check out some of these references:

Facebook0 Tweet0

Quicksort algorithm – Lomuto partition scheme8 min read