Understand Tree Traversal: Pre-order, In-order, and Post-order Traversal

Many of you probably have familiar with arrays or linked-lists, we know that in those data structures, elements can be traversed linearly. But what about the binary tree? As we can presume, the binary tree is a non-linear data structure, which means within hand one item we can reach out to several other items at the same time, e.g if you have a parent node you can access it to its left and right child if existed.

Because of this, there are not just once, but several techniques can be applied to traverse the tree. The most ubiquitous ones are pre-order traversal, in-order traversal, post-order traversal and level-order traversal (Breadth First Traversal).

Firstly, for better envision, let’s draw some examples real quick:

In this article, we’re going to dive deep into In-order, Pre-order, Post-order traversals in Binary Search Tree and understand how they work in a recursive manner.

But before we go, if you already know about recursion, how it works, what is the call stack and activation record then it’s a great help.

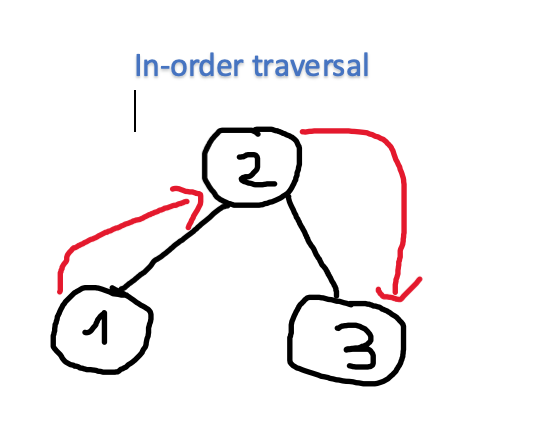
In-order Traversal

What do I mean by traversing the tree?

Tree traversal is a process of exploring all the nodes in the tree only once. You can either implement in-order traversal iteratively or recursively. However, we’re interested in doing this with recursion.

With in-order traversal, the left child is explored first, next visiting the root and then visit the right child. With that in mind, we are gonna implement a recursive procedure with the following steps:

Recursively visit the left subtree
Visit the node
Recursively visit the right subtree

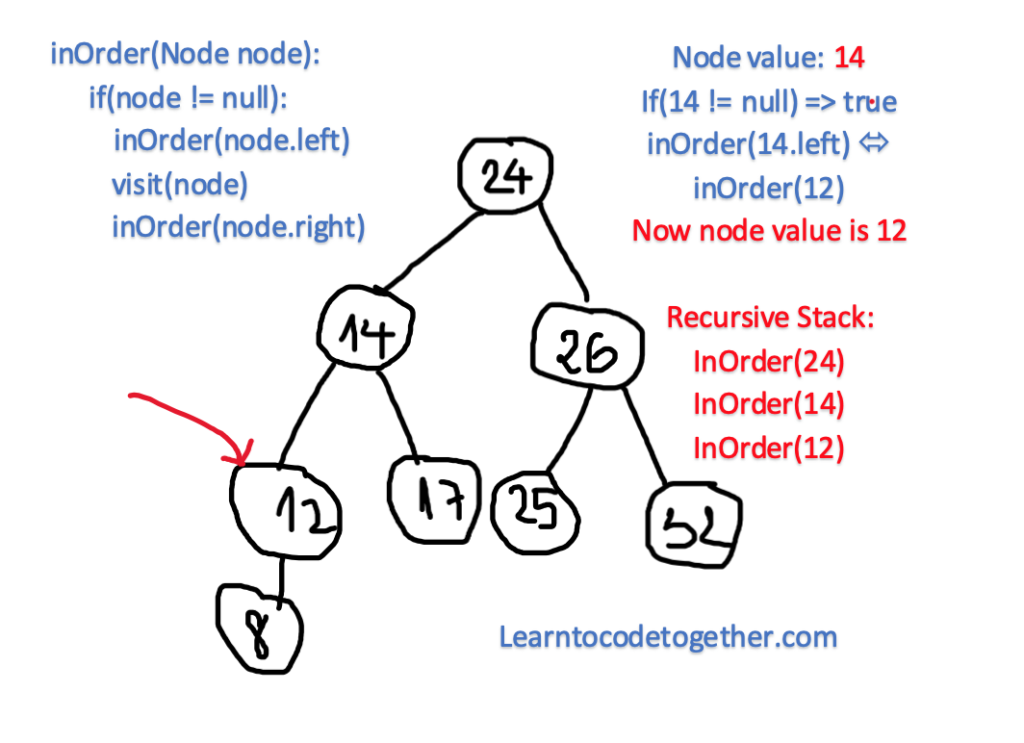
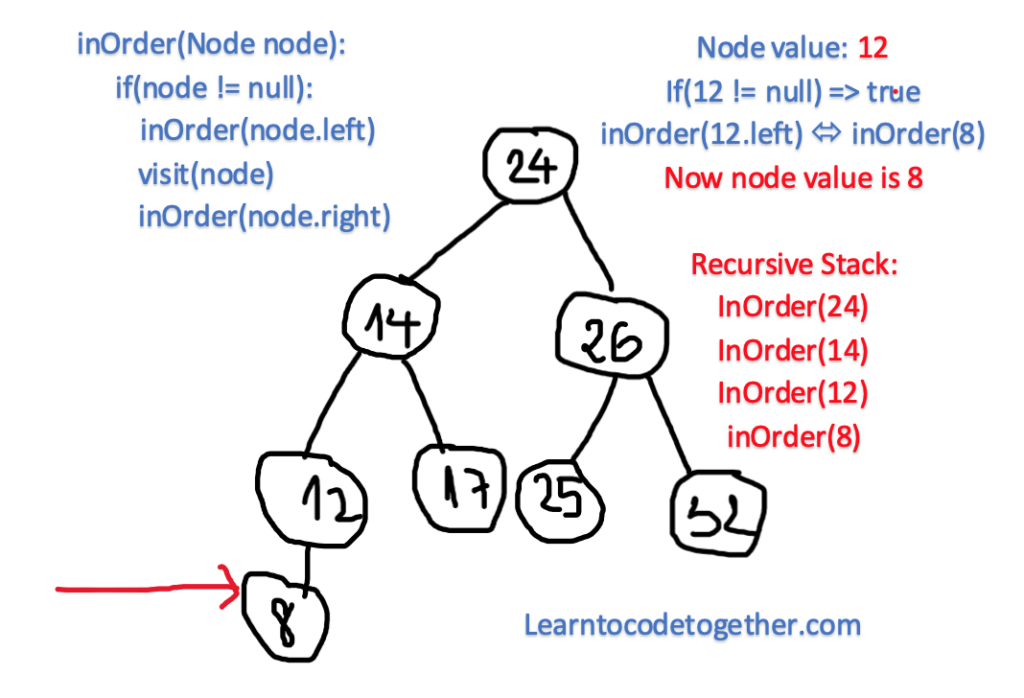
What do I mean by “recursively visit” left or right subtree and why it does not “visit” those positions? Let’s see another example:

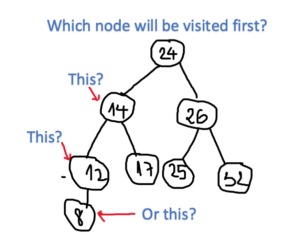
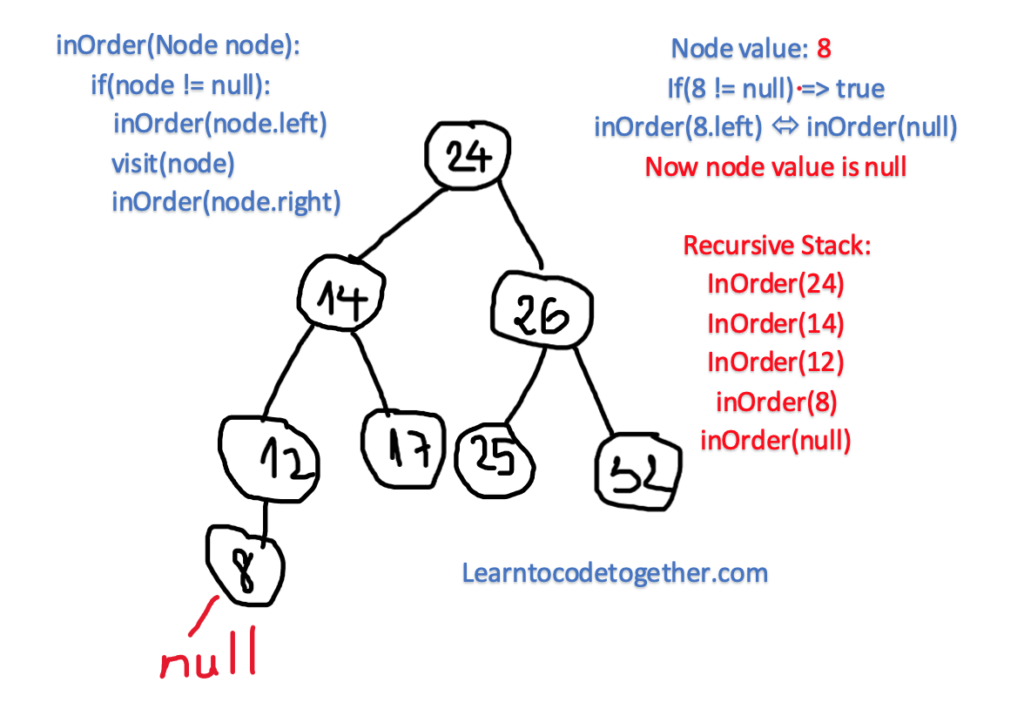
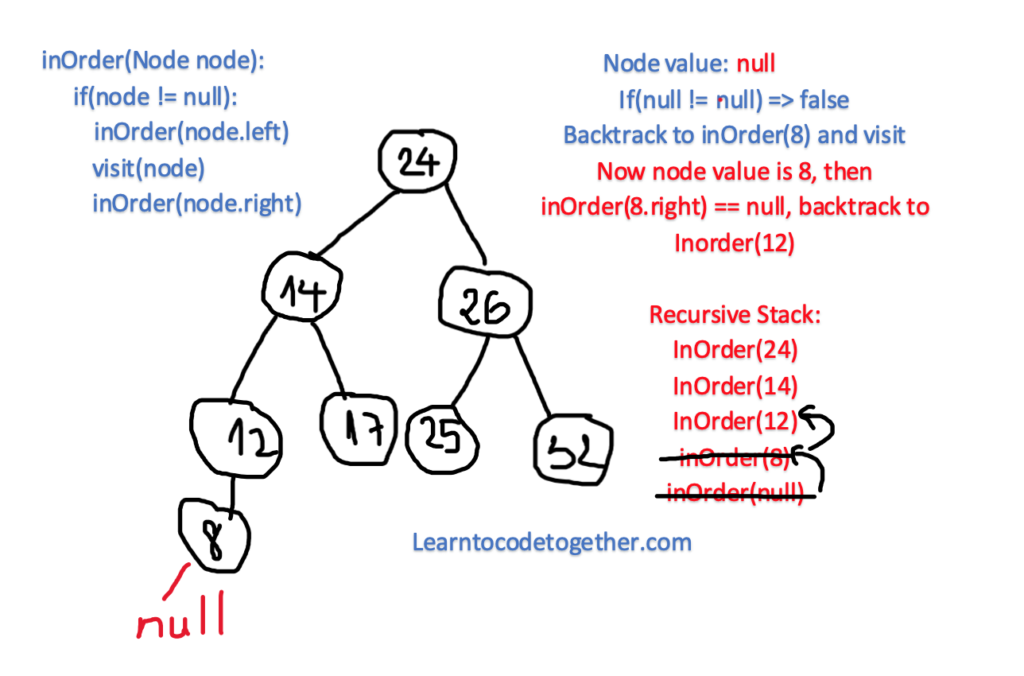
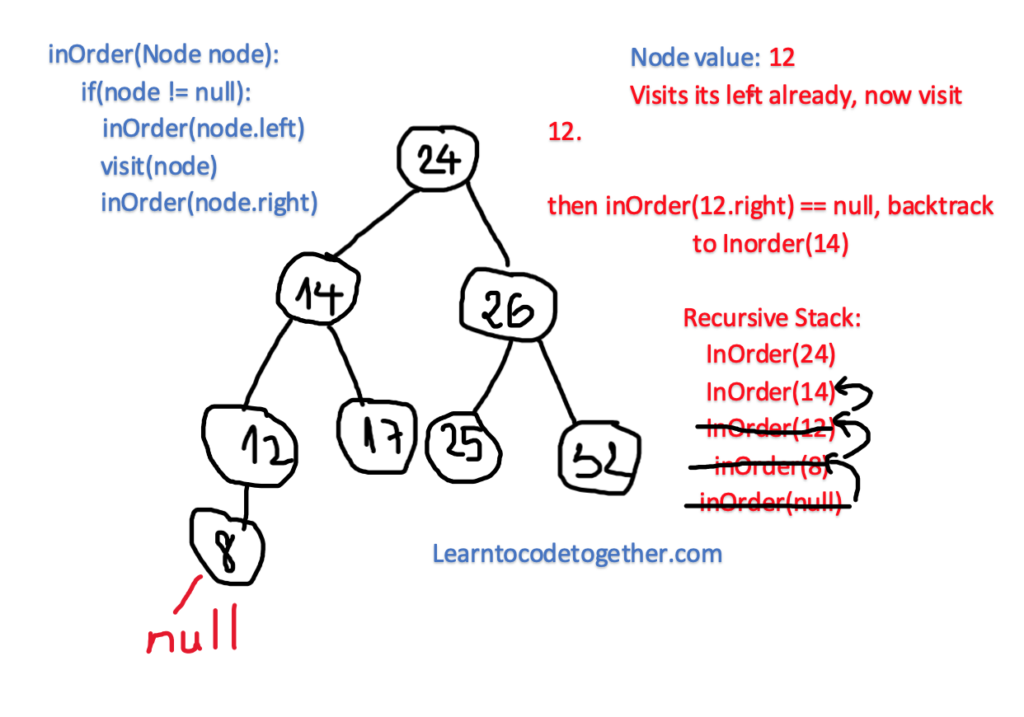
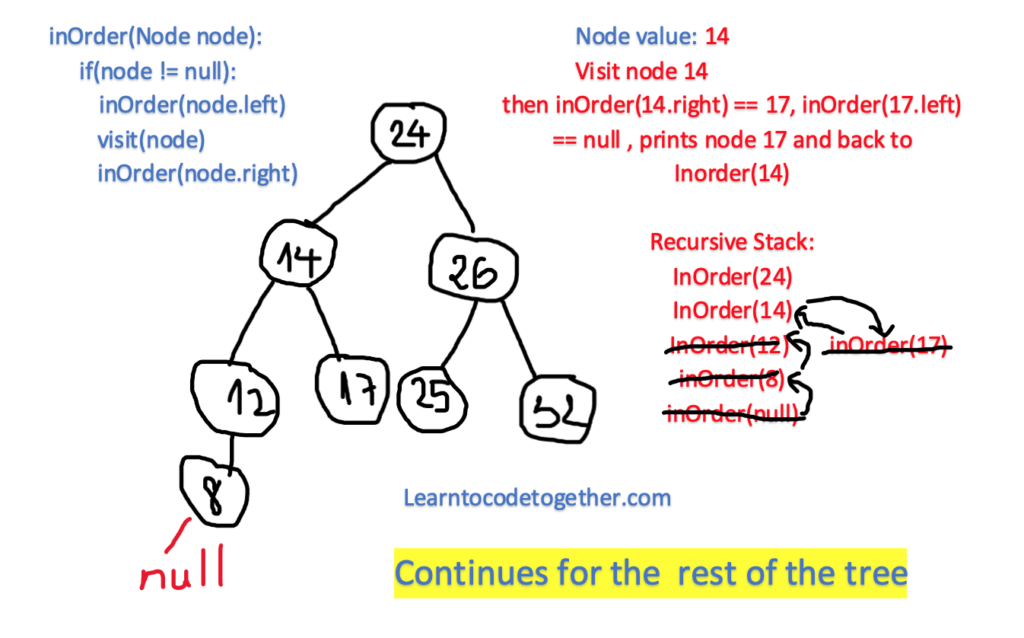
The node with the value of 24 is the root of the tree, but it has 4 children on the left, which are 14, 12, 17 and 8. Which is it going to be visited first? The answer is the last one. Initially, it gets to the root node 24, then it recursively exploring the left, here in the left child 14, but here the recursion is again applied, it continues to go to the left node of 14, which is 12, then here in 12, it again traverses the left part, finds the value of 8, but here it no longer can explore deeper, then the algorithm stops, prints the value of 8, then go back for the previous call of recursion which is not yet done, print the Node of 12, then it goes back to print the Node 12, then here in 12, it exerts to attain the right child of this node but there is nothing, then it backtracks to the node 14, this procedure is continued again and again until there is nothing left.

During an inorder traversal, we visit a position between the recursive traversal of its left and right subtrees. The inorder traversal of a binary tree T can be informally viewed as visiting the nodes of T “from left to right.”

For now, let’s meticulously finalized the in-order traversal method with the recursive approach:

Create a method named inOrder(Node node). The recursive function keeps doing while the node is not null
Recursively call inOrder(node.left) in its left child
Perform the “visit” action for the position node
Recursively call inOrder(node.right) in its right child

private void inOrder(Node node) {
      if (node != null) {
          /** recursively calls inOrder on the left sub-tree */
          inOrder(node.left);
          /** prints the value at the current node */
          System.out.println("The current node value is " + node.element);
          /** recursively calls inOrder method for the right subtree. */
          inOrder(node.right);
      }

  }

Let’s recall the example I have given at the beginning of this section, put it to this method and see what happens:

          24
         /  \
       14    26
      /  \    / \
     12   17  25 32
    /
   8

Output:

8, 12, 14, 17, 24, 25, 26, 32

Here we mark inOrder as a private method and we gonna use a method that accepts no parameters calls inOrder method for public use. By doing so, the work of in-order algorithms is done internally and we don’t have to worry about the node we pass in when going outside the scope of this method:

public void inOrderTraversal() {
    inOrder(root);
}

The root variable we pass here in the inOrderTraversalPublic is an instance variable that is already defined in the class which contains those 2 methods. The complete code of this class is now shown below:

class BST<T extends Comparable<T>> {
  private Node root = null;
  private int nodeCount = 0;

  private class Node {
      T element;
      Node left, right;

      public Node(Node left, Node right, T element) {
          this.left = left;
          this.right = right;
          this.element = element;
      }
  }
  /** Utility method for adding element to the BST. */
  private Node insert(Node node, T value) {
      if (node == null) {
          node = new Node(null, null, value);
      }
      else if (value.compareTo(node.element) < 0) {
          node.left = insert(node.left, value);

      }
      else if (value.compareTo(node.element) > 0) {
          node.right = insert(node.right, value);
      }
      else if (value.compareTo(node.element) == 0) {
          return null;
      }
      return node;

  }

  public void add(T value) {
      root = insert(root, value);
      nodeCount++;
  }

  /** Our work is here, the in-order traversal method in BST. */
  private void inOrder(Node node) {
      if (node != null) {
          inOrder(node.left);
          System.out.println(node.element);
          inOrder(node.right);
      }

  }
  /** method with no parameter */
  public void inOrderTraversal() {
      inOrder(root);
  }
  /** Test in-order traversal */
  public static void main(String[] args){
    BST<Integer> tree = new BST<>();
    tree.add(24);
    tree.add(14);
    tree.add(12);
    tree.add(8);
    tree.add(17);
    tree.add(26);
    tree.add(25);
    tree.add(32);
    tree.inOrderTraversal();
    /** Output: 8, 12, 14, 17, 24, 25, 26, 32 */

  }
}

As we implement the in-order traversal algorithm in a Binary Search Tree, hence the interesting property which is easy to notice that the output is sorted in the ascending order. Besides this, the in-order traversal algorithm can be used in binary trees to represent arithmetic expressions.

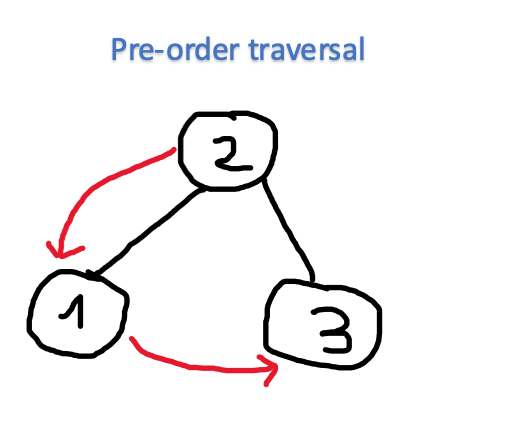
Pre-order Traversal

For now, if we already have an idea about how the in-order traversal works in the binary tree, we can flexibly adapt to another type of traversal, which is the pre-order traversal, in the pre-order traversal, we explore the tree as follow:

Visit the node
Recursively explore the left subtree
Recursively explore the right subtree

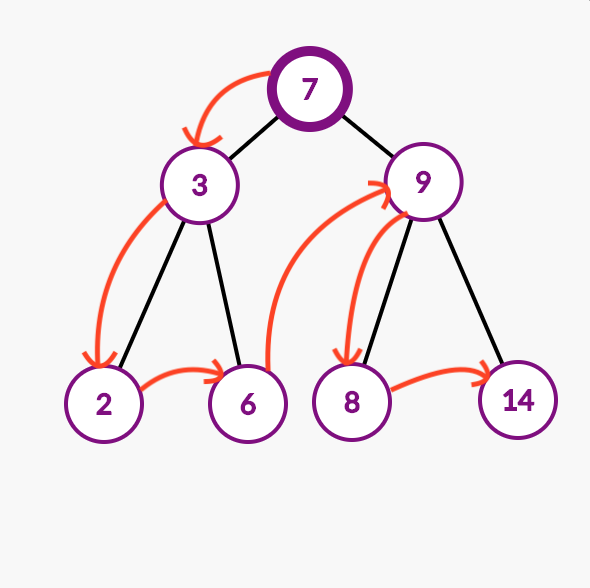
If we employ the pre-order traversal to this example above, here is how the tree is sequentially visited:

7 -> 3 -> 2 -> 6 -> 9 -> 8 -> 14

Here we just change the order of the visit, in this traversal, the root of the tree always is visited first before any recursion, here is our code for this implementation:

private void preOrder(Node node) {
      if(node != null){ 
      System.out.println("Currently visit the node: " + node.element); // visit the current root node
      preOrder(node.left); // recursively visits the left subtree
      preOrder(node.right); // recursively visits the right subtree
      }
  }

For simplifying the usage, let’s define a public preOrderTraversal() method which accepts no argument:

public void preOrderTraversal() { 
    preOrder(root);
}

In this public method, we just simply call the preOrder function and pass in the root which is an instance variable we already defined in the class. Now, let’s test this program:

 public static void main(String[] args){
    BST<Integer> tree = new BST<>();
    tree.add(7);
    tree.add(3);
    tree.add(9);
    tree.add(2);
    tree.add(6);
    tree.add(8);
    tree.add(14);
    tree.preOrderTraversal();
}

Output:

Currently visit the node: 7
Currently visit the node: 3
Currently visit the node: 2
Currently visit the node: 6
Currently visit the node: 9
Currently visit the node: 8
Currently visit the node: 14

The complete code of the pre-order traversal can be found here.

Pre-order traversal can have many applications, it is topologically sorted, which means the parent is always processed before any of its child nodes. This property can be applied for scheduling a sequence of jobs or tasks.

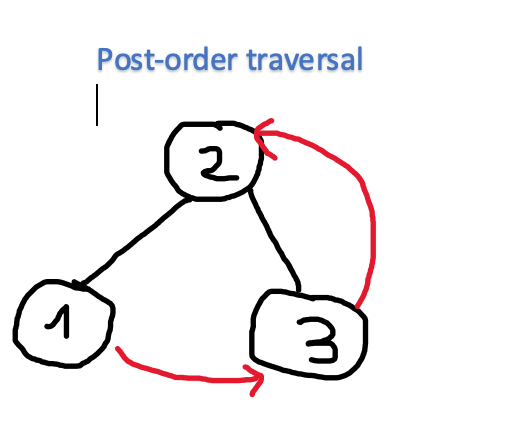
Post-order Traversal

Last, we examine the post-order traversal. Again, we just have to change the order of the visit, this technique can be viewed as follow:

Recursively visit the left subtree
Recursively visit the right subtree
Visit the node

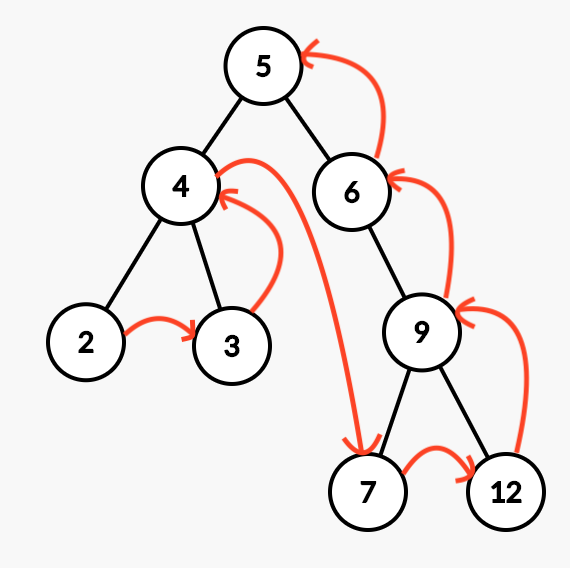
In contrast to pre-order traversal, the root of the tree always is visited last after recursively visit the left and the right subtrees. If we take the image above as an example, then the order will as follow:

2 -> 3 -> 4 -> 7 -> 12 -> 9 -> 6 -> 5

private void postOrder(Node node) {
        if (node != null) {
            postOrder(node.left);
            postOrder(node.right);
            System.out.println("Currently visit the node: 
 " + node.element);
        }
}

And afterward, we define a public method named postOrderTraversal:

public void postOrderTraversal(){
        postOrder(root);
}

public static void main(String[] args) {
        BST<Integer> bst = new BST<>();
        bst.add(5);
        bst.add(4);
        bst.add(3);
        bst.add(2);
        bst.add(6);
        bst.add(9);
        bst.add(7);
        bst.add(12);
        bst.postOrderTraversal();
 }

Output:

Currently visit the node: 2
Currently visit the node: 3
Currently visit the node: 4
Currently visit the node: 7
Currently visit the node: 12
Currently visit the node: 9
Currently visit the node: 6
Currently visit the node: 5

The post-order traversal has several applications, it can be used to deleting or freeing nodes and values for an entire binary tree. The post-order traversal can also generate a postfix representation of a binary tree.

Summing up

In this article, we have learned about 3 types of traversal in a binary tree, which are pre-order, in-order, and post-order traversals. All 3 of them can be implemented by using recursion and their common property is all visiting the child nodes of the sub-tree first before visiting the siblings, hence they are also called Depth-First Traversal.

Pre-order, In-order or Post-order imply how the tree will be visited with respect to the root node. For the pre-order, the root will be visited first after any recursion. With the in-order, the root always is visited after the left subtree and before the right subtree. For post-order traversal, the root is visited last in contrast with pre-order. Each one has its own perks and can be applied in many applications.

The time complexity of those 3 traversal algorithms is $O(n)$ . Fully implementation and explanation of BST can be found here, the code for tree traversals covered in this article can be found here.

0 0 votes

Article Rating

Facebook Tweet

Understand Tree Traversal: Pre-order, In-order, and Post-order Traversal11 min read

In-order Traversal

Pre-order Traversal

Post-order Traversal

Summing up